A Cauchy sequence is a sequence whose terms become very close to each other as the sequence go further. Cauchy sequence is helps in study of two topics
1. In real number
2. In metric space
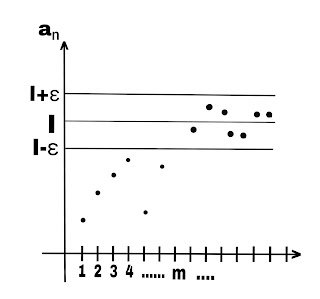
Definition:- A sequence {xₙ} is said to be Cauchy sequence if given ε>0, however small, ∃ a positive integer k(depending upon ε) such that
1. In real number
2. In metric space
Cauchy sequence
In real number
Definition:- A sequence {xₙ} is said to be Cauchy sequence if given ε>0, however small, ∃ a positive integer k(depending upon ε) such that
Another definition:- A sequence {xₙ} is said to be Cauchy sequence if given ε>0, however small, ∃ a positive integer m(depending upon ε) such that
In given figure, we have taken n as subscript on x-axis and xₙ on y-axis. when n,m≥k, take
Article 1:- Prove that a Cauchy sequence is bounded.
proof: Let {xₙ} be Cauchy sequence.
given ε>0, there exist a positive integer p such that
In particular,
Now
Let
| xₙ |≤M ∀ n
⇒ {xₙ} is bounded
Article 2:- Prove that a convergent sequence is always a Cauchy sequence.
Proof: Let the sequence {xₙ} converge to l
given ε>0, however small, ∃ k∈ℕ s.t
Let m≥k be a natural number.
Now
{xₙ} is a Cauchy sequence.
From artical2 it is clear that when ever a sequence is Cauchy sequence, it is convergent to.
In Metric space
Definition:- A sequence {pₙ} in a metric space X is said to be a Cauchy sequence if for every ε>0 there is an integer N such that
Definition:- Let E be a non empty subset of metric space X, and let S be the set of all real number of the form d(p,q), with p∈E and q∈E. The sup of S is called the diameter of E.
If {pₙ} is a sequence in X and if Eₙ consist of the point
Definition:- A metric space in which every Cauchy sequence converges is said to be complete.
Thus every Cauchy sequence in E is a Cauchy sequence in X, hence it converge to some p∈X, and actually p∈E since E is closed. An example of metric space which is not complete is the space of all rational number, with d(x,y)=| x-y |.
It shows that convergent sequence are bounded, but that bounded sequence in Rⁿ need not converge. However, there is one important case in which convergence is equivalent to boundedness; this happen for monotonic sequence in R¹.