The infimum and supremum are concepts in mathematical analysis. It helps in study of two subjects. It describe the minimum and maximum of finite set. The limit of the infimum and supremum used in some convergence sequence and in particular in computation of domain of convergence of power series.
To understand the concept of infimum(glb) and supremum(lub), you first have to understand what is upperbound and lower bound.
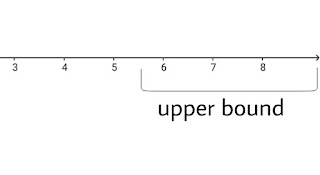
Upper bound:- Let S be a non-empty subset of real number.
If there exist a real number K such that x≤k ∀ x∈S
then k is said to be an upper bound of S the set S is said to be bounded above or bounded to the right.
Meaning:- It means that if x∈R then there always exist a number which is greater than x.
Example:- If x=5 then take k=6,7,8,9..... they are all upper bound of x and are greater then 5.
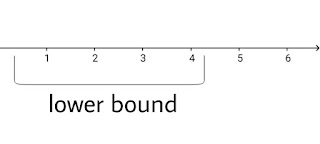
Lower bound. If there exist a real number l such that l≤x ∀ x∈S
Then l is said to be lower bound of S. The set S is said to be bounded below or bounded to the left if it has a lower bound.
Meaning:- It means that if x∈R then there exist a number which is lower then x.
Example:- If x=5 then take l=4,3,2,1..... they are all lower bound of x and are lower then 5.
Let S be a non-empty subset of R which is bounded above. Then there exist a real number u which is the smallest of all upper bound of S i.e, for other upper bound u´ of S we have u≤u´.
This number u is called the least upper bound of S or supremum of S.
Meaning:- Least upper bound of a set S bounded above is unique. For, if u and u´ are two least upper bound of S, then by definition, u≤u´ and u´≤u which implies that u=u´.
Let S be a non-empty subset of R which bounded below. Then there exist a real number l which is the greatest of all the lower bound of S i.e., for any other lower bound l´ of S we have l´≤ l
This number l is called the greatest lower bound of S or infimum of S.
Example. if x∈[-3,10]
-3≤x≤10
glb=-3, lub=10
Definition:- If N is a set of natural number and X is any set, then a function f: N→X is called a sequence.
Let a: N→R be a sequence. The image of n∈N is denoted by aₙ. thus a₁,a₂,a₃....... are the real number associated to 1,2,3....... by this mapping aₙ is called the general term or the n term of the sequence.
bounded above=A sequence {aₙ} is said to be bounded above if there exist a real number k such that aₙ≤k ∀ n∈N
k is called an upper bound of the sequence {aₙ}.
bounded below=A sequence {aₙ} is said to be bounded below if there exist a real number h such that h≤aₙ n∈N. h is called a lower bound of the sequence {aₙ}.
bounded sequence=A sequence {aₙ} is said to be bounded if it is a bounded above as well as bounded below i.e., if there exist two real number h and k such that
h≤aₙ≤k ∀ n∈N.
supremum(lub)
1. aₙ≤u ∀ n∈N.
2. Given ε>0 however small,∃ at least one positive integer m such that a >u-ε.
>u-ε.
infimum(glb)
1. aₙ≥l ∀n∈N.
2. Given ε>0 however small, ∃ at least one positive integer m such that <l+ε.
<l+ε.
In set theory
To understand the concept of infimum(glb) and supremum(lub), you first have to understand what is upperbound and lower bound.
Upper bound:- Let S be a non-empty subset of real number.
If there exist a real number K such that x≤k ∀ x∈S
then k is said to be an upper bound of S the set S is said to be bounded above or bounded to the right.
Meaning:- It means that if x∈R then there always exist a number which is greater than x.
Example:- If x=5 then take k=6,7,8,9..... they are all upper bound of x and are greater then 5.
Lower bound. If there exist a real number l such that l≤x ∀ x∈S
Then l is said to be lower bound of S. The set S is said to be bounded below or bounded to the left if it has a lower bound.
Meaning:- It means that if x∈R then there exist a number which is lower then x.
Example:- If x=5 then take l=4,3,2,1..... they are all lower bound of x and are lower then 5.
Supremum (least upper bound)
Let S be a non-empty subset of R which is bounded above. Then there exist a real number u which is the smallest of all upper bound of S i.e, for other upper bound u´ of S we have u≤u´.
This number u is called the least upper bound of S or supremum of S.
Meaning:- Least upper bound of a set S bounded above is unique. For, if u and u´ are two least upper bound of S, then by definition, u≤u´ and u´≤u which implies that u=u´.
Infimum (greatest lower bound)
Let S be a non-empty subset of R which bounded below. Then there exist a real number l which is the greatest of all the lower bound of S i.e., for any other lower bound l´ of S we have l´≤ l
This number l is called the greatest lower bound of S or infimum of S.
Example. if x∈[-3,10]
-3≤x≤10
glb=-3, lub=10
Sequence
Definition:- If N is a set of natural number and X is any set, then a function f: N→X is called a sequence.
Let a: N→R be a sequence. The image of n∈N is denoted by aₙ. thus a₁,a₂,a₃....... are the real number associated to 1,2,3....... by this mapping aₙ is called the general term or the n term of the sequence.
bounded and unbounded sequence
bounded above=A sequence {aₙ} is said to be bounded above if there exist a real number k such that aₙ≤k ∀ n∈N
k is called an upper bound of the sequence {aₙ}.
bounded below=A sequence {aₙ} is said to be bounded below if there exist a real number h such that h≤aₙ n∈N. h is called a lower bound of the sequence {aₙ}.
bounded sequence=A sequence {aₙ} is said to be bounded if it is a bounded above as well as bounded below i.e., if there exist two real number h and k such that
h≤aₙ≤k ∀ n∈N.
supremum(lub)
1. aₙ≤u ∀ n∈N.
2. Given ε>0 however small,∃ at least one positive integer m such that a
infimum(glb)
1. aₙ≥l ∀n∈N.
2. Given ε>0 however small, ∃ at least one positive integer m such that











This article is very informative. It is very useful for me thanks for sharing this great information and useful Top 10 Schools In Chennai
ReplyDelete