When you plot a function in the graph, if the curve opens towards the positive Y-axis then it is said to be concave up (or convex down) function while if it opens downwards then the curve is said to be concave down (or convex up ) function.
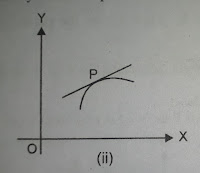
Consider the curve y=f(x) in [ a,b ]. Let it be continuous and possessing tangent at every point in ( a,b ).
Draw a tangent at any point P ( c,f(c) ) on the curve. Let us assume that this tangent is not parallel to Y-axis so that f'(c) is some finite number.
Now there are three mutually exclusive possibilities to consider.
As x-increase, f'(x) is either of the same sign and increasing or change sign from -ve to +ve. In either case, the slop f'(x) is increasing and f''(x) >0. Such graphs are bending upward or the portion lies above the chord.
A portion of the curve on both side of P, however small it may be, lies below the tangent at P ( i.e. towards the -ve direction of Y-axis ). In this case, we say that the curve is convex upward or concave downward at P.
As x-increase, f'(x) is either of the same sign and decreasing or change sign from +ve to -ve. In either case, the slop f'(x) is decreasing and f''(x) <0. Such graphs are bending downward or the portion lies below the chord.
The portion of the curve on the two side of P lies on different side of the tangent at P i.e, the curve crosses the tangent at P. In this case we say that P is a point of inflection on the curve.
So, at a point of inflection the curve change from concave upward so convex downward or vice-versa.
So at a point of inflection f''(x)=0.
(1). Evaluate
(2). Find the interval ( a,b ) for which .
.
Then ( a,b ) is the interval of being convex downward.
(3). Find the interval ( a,b ) for which .
.
Then ( a,b ) is the interval of being convex upward.
Q1. Prove that the curve is concave upward for all x∈ℝ.
is concave upward for all x∈ℝ.
Sol.
Here

and
Concavity and convexity
Consider the curve y=f(x) in [ a,b ]. Let it be continuous and possessing tangent at every point in ( a,b ).
Draw a tangent at any point P ( c,f(c) ) on the curve. Let us assume that this tangent is not parallel to Y-axis so that f'(c) is some finite number.
Now there are three mutually exclusive possibilities to consider.
1. Concave upward
A portion of the curve on both side of P, however small it may be, lies above the tangent at P ( i.e. towards the +ve direction of Y-axis ). In this case, we say that the curve is concave upward or convex downward at P. Such curve "hold water".As x-increase, f'(x) is either of the same sign and increasing or change sign from -ve to +ve. In either case, the slop f'(x) is increasing and f''(x) >0. Such graphs are bending upward or the portion lies above the chord.
2. Concave downward
A portion of the curve on both side of P, however small it may be, lies below the tangent at P ( i.e. towards the -ve direction of Y-axis ). In this case, we say that the curve is convex upward or concave downward at P.
As x-increase, f'(x) is either of the same sign and decreasing or change sign from +ve to -ve. In either case, the slop f'(x) is decreasing and f''(x) <0. Such graphs are bending downward or the portion lies below the chord.
3. Point of inflection
The portion of the curve on the two side of P lies on different side of the tangent at P i.e, the curve crosses the tangent at P. In this case we say that P is a point of inflection on the curve.
So, at a point of inflection the curve change from concave upward so convex downward or vice-versa.
So at a point of inflection f''(x)=0.
☆Definition of concavity and convexity
A curve is said to be concave downward ( or convex upward ) on the interval ( a,b ) if all the points of the curve lies below any tangent to it on that interval. It is said to be concave upward ( or convex downwards ) on the interval ( a,b ) if all the points of the curve lies above any tangent to it on that interval.☆Working method for concavity and convexity
(1). Evaluate
(2). Find the interval ( a,b ) for which
Then ( a,b ) is the interval of being convex downward.
(3). Find the interval ( a,b ) for which
Then ( a,b ) is the interval of being convex upward.
Examples
Q1. Prove that the curve
Sol.
Here
and
The curve
Q2. Prove that the curve
Sol.
Here
Now
Hence the curve is concave downward or convex upward for x >0.













This is a thoughtful and clear explanation of concavity and convexity two concepts that many students initially find abstract. I appreciate how the post breaks down the ideas with simple reasoning and practical interpretation. It really helps connect theory to visual understanding. When I was studying these topics, I often struggled until I sought online statistics assignment help which made the learning process smoother. Posts like this are valuable because they make challenging mathematical ideas far more approachable.
ReplyDelete