The convergence sequence is the value, sequence approaches as the number of terms goes to infinity. Not every sequence is convergent. The sequence whose nth term approaches are called convergent while those that don't are called divergent. To understand what convergent is you first have to understand what sequence is?.
Definition:- If ℕ is a set of natural number and X any set, then a function f :ℕ→X is called sequence.
If X=ℝ or a subset of ℝ, then f is called a real sequence and if X=ℂ or a set of ℂ, then f is called a complex sequence.
Let a :ℕ→ℝ be a sequence. The image of n∈ℕ, instead of being denoted by a(n) is generally denoted by aₙ thus a₁a₂a₃a₄....... are the real number associated to 1 2 3 4.....by this mapping aₙ is called the general term or the nth term of the sequence.
Examples of sequence
1. The sequence {aₙ} where aₙ=n is {1,2,3,...n,....}
2. The sequence {aₙ} where is {
is { }
}
3.The sequence {aₙ} where aₙ=(-1)ⁿ is {-1,1,-1,1,-1,.....}
A sequence {aₙ} is said to converge to a limit l, if given ε>0 however small there exist a positive integer m(depending upon ε) such that
|aₙ-l|<ε ∀ n≥m
l is called a limit of sequence {aₙ} and we write it as

or aₙ→l as n→∞ or simply aₙ→l
We know that |aₙ-l|<ε ⇒ aₙ∈(l-ε,l+ε). Now a neighbourhood V of l always contain (l-ε,l+ε). Thus we gives another definition of convergent sequence.
A sequence {aₙ} is said to converge t a limit l if given a neighbourhood V of l, there exist aₙ integers m such that aₙ∈V ∀n≥m
Meaning:- At a point when n become greater than m(n≥m). Then every term of aₙ reaching to a particular value. Then we call it as {aₙ} converges to l.
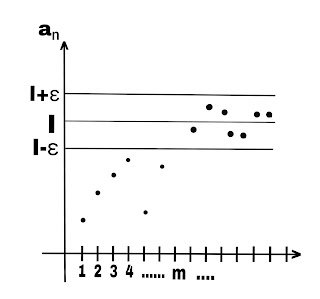
In the figure, aₙ is taken on y-axis and its subscript on x-axis. It show that if all the terms after m lies between (l-ε,l+ε) then sequence {aₙ} converges to l.
For example the sequence converge to 0
converge to 0
Sequence
Definition:- If ℕ is a set of natural number and X any set, then a function f :ℕ→X is called sequence.
If X=ℝ or a subset of ℝ, then f is called a real sequence and if X=ℂ or a set of ℂ, then f is called a complex sequence.
Let a :ℕ→ℝ be a sequence. The image of n∈ℕ, instead of being denoted by a(n) is generally denoted by aₙ thus a₁a₂a₃a₄....... are the real number associated to 1 2 3 4.....by this mapping aₙ is called the general term or the nth term of the sequence.
Examples of sequence
1. The sequence {aₙ} where aₙ=n is {1,2,3,...n,....}
2. The sequence {aₙ} where
3.The sequence {aₙ} where aₙ=(-1)ⁿ is {-1,1,-1,1,-1,.....}
Convergence sequence
A sequence {aₙ} is said to converge to a limit l, if given ε>0 however small there exist a positive integer m(depending upon ε) such that
|aₙ-l|<ε ∀ n≥m
l is called a limit of sequence {aₙ} and we write it as
or aₙ→l as n→∞ or simply aₙ→l
We know that |aₙ-l|<ε ⇒ aₙ∈(l-ε,l+ε). Now a neighbourhood V of l always contain (l-ε,l+ε). Thus we gives another definition of convergent sequence.
A sequence {aₙ} is said to converge t a limit l if given a neighbourhood V of l, there exist aₙ integers m such that aₙ∈V ∀n≥m
Meaning:- At a point when n become greater than m(n≥m). Then every term of aₙ reaching to a particular value. Then we call it as {aₙ} converges to l.
In the figure, aₙ is taken on y-axis and its subscript on x-axis. It show that if all the terms after m lies between (l-ε,l+ε) then sequence {aₙ} converges to l.
For example the sequence











0 comments:
Post a Comment