Interval is a way to describe continuous set of real number by the number that bound them. However, they are not meant to denote a specific point. Rather, they are meant to describe an inequality or system of inequalities.
Let a and b be two distinct real number with a<b then,
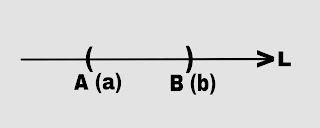
The set of all real number between a and b said to form an open interval from a to b denoted by (a,b). In symbols
Let a and b be two distinct real number with a<b then,
1. Open interval
The set of all real number between a and b said to form an open interval from a to b denoted by (a,b). In symbols
Geometrically the open interval (a,b) is represented on the real line as
For example= Inequality: -1<x<5
Interval : (-1,5)
In this case, x does not equal -1 and 5. When both of the end point are excluded from the interval, the interval is open interval.
2. Closed interval
The set of all real number between a and b including the end points and b is said to form a closed interval and is denoted by [a,b].
In symbols
Geometrically, the closed interval [a,b] is represented on the real line as
For example= inequality: 3≤x≤9
interval : [3,9]
In this case, x could equal 3 or 9 when both of the end point are included in the interval, the interval is a closed interval.
3. Half-open intervals
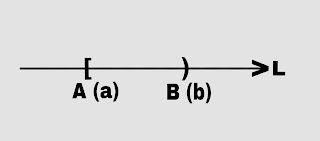
An interval in which one end point is included are the other end is excluded is called half-open interval.
In symbols,
Geometrically, [a,b) is represented on the line as
For example= inequality: -3≤x<5
interval : [-3,5]
In this case, x could equal -3 but it cannot equal 5. When one of the end points is included in the interval but the other is not, the the interval is a half-open interval.
Similarly
Geometrically, (a,b] is represented on the real line as
The interval defined above are called finite intervals. Now we define infinite intervals.
Infinite interval. The set of all real number x such that x>a forms an infinite set and is denoted by (a,∞).
Symbolically
If an interval has no lower bound or upper bound then the -∞ and ∞ symbol are used. These symbols are always used with a parentheses bracket, because infinity is not a number that can be included in a set
For example. inequality: x≤7
interval : (-∞,7)
inequality: x>3
interval : (3,∞).














0 comments:
Post a Comment