Rectification of curve ~ Easy to understand maths

Rectification is the process of finding the length of an arc of a curve between two given points. The arc length formula uses the language of calculus to generalize and solve a classical problem in geometry : finding the length of a specific curve.

Given a function $f$ that is defined and differentiable on the interval $\left [ a,b \right ]$ , the length L of the curve $y=f(x)$ in that interval is

$L=\int_{a}^{b}\sqrt{1+\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^{2}}\, \: dx.$

Curve : Let $f$ be continuous function on $\left [ a,b \right ]$ . Then the graph of $f$ on $\left [ a,b \right ]$ i.e, ${\: (x,f(x)) : a\leq x\leq b\: }$ is called a curve.

Length of the curve: Let AB the curve defined by continuous function $y=f(x)$ on $\left [ a,b \right ]$ .

Let $P=\left \{ a=x_{0},x_{1},x_{2},......x_{n-1},x_{n}=b \right \}$ be the partition of $\left [ a,b \right ]$ into n equal parts each length h, where

$h=\frac{b-a}{n}$
Let $L_{n}$ denote the sum of the length of segments of broken lines, then

$L_{n}=\sum_{n}^{i=1}\left | P_{i-1} P_{i} \right |$
If $\lim_{n\rightarrow \infty }L_{n}$ exist, then it is called length of the curve and is denoted by L. The number L, if exist, is unique.

Rectifiable curve : A continuous curve, which has length, is called rectifiable.

Rectification : The process of finding the length of an arc of a curve between two given points is called rectification.

1. Arc formula for cartesian equation

If C is curve defined by $y=f(x)$ , where $f$ has a continuous derivative f'(x) an $\left [ a,b \right ]$ , then the length of the curve C is given by
$\int_{a}^{b}\sqrt{1+\left (f'(x))^{2}}\, \: dx.$
Or
$\therefore \: \: Length \: of \: curve\: C =\int_{a}^{b}\sqrt{1+\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^{2}}\, \: dx.$

2. Length of an arc of a plan curve with parametric equation

Let C is curve defined by parametric equation $x=f(t),\: y=g(t),\: \alpha \leq t\leq \beta$ and $f'(t)\neq 0\: \: \forall\,\: t\: \epsilon \left [ \alpha ,\beta \right ]$ , then length L of curve C is given by

$L=\int_{a}^{b}\sqrt{ \left ( \frac{\mathrm{d} x}{\mathrm{d} t} \right )^{2}+\left ( \frac{\mathrm{d} y}{\mathrm{d} t} \right )^{2}}\, \: dt.$

3. Length of an arc of a plan curve with polar equation

1. If a function $f$ has continuous derivative on $[ \alpha ,\beta ]$ , then the length L of the arc of the curve $r=f(\Theta )$ from the point $\Theta =\alpha$ to the point $\Theta =\beta$ is given by

$L=\int_{\alpha }^{\beta }\sqrt{r^{2}+\left ( \frac{\mathrm{d} r}{\mathrm{d} \Theta } \right )^{2}}\, \: d\Theta .$

2. If a function $f$ has continuous derivative on $\left [ a,b \right ]$ , then the length L of the arc of the curve $\Theta =f(r)$ from the point $r=a$ to the point

$r=b$ is given by

$L=\int_{a}^{b }\sqrt{1+r^{2}\left ( \frac{\mathrm{d} \Theta }{\mathrm{d} r } \right )^{2}}\, \: dr.$

Example

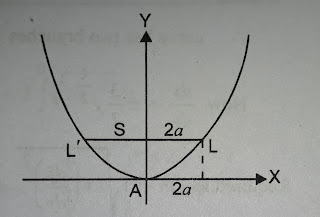
Q1. Find the length of the arc of the parabola $x^{2}=4ay$ extending from the vertex to one extremity of the latus rectum.
Sol.
The equation of the parabola is $x^{2}=4ay$
Let A be the vertex and L one extremity of the latus rectum.

Now $y=\frac{x^{2}}{4a}$

$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{1}{4a}(2x)=\frac{x}{2a}$

$\therefore\: \: \: arc\: \: AL =\int_{0}^{2a}\sqrt{1+\left ( \frac{\mathrm{d} y}{\mathrm{d} x} \right )^{2}}\, \: dx.$

$=\int_{0}^{2a}\sqrt{1+\left ( \frac{x^{2}}{4a^{2}} \right )}\, \: dx.=\frac{1}{2a}\int_{0}^{2a}\sqrt{4a^{2}+x^{2}}dx$

$=\frac{1}{2a}\left [ \frac{x\sqrt{(2a)^{2}+x^{2}}}{2}+\frac{(2a)^{2}}{2}\sinh ^{-1}\frac{x}{2a} \right ]_{0}^{2a}$

= $\frac{1}{4a}\left [ 2a.2\sqrt{2}a+4a^{2}\sinh ^{-1} 1 -0(0+4a^{2}.0)\right ]$

= $\frac{4a^{2}}{4a}\left [ \sqrt{2} +\sinh ^{-1}1\right ]=a\left [ \sqrt{2} +\log (1+\sqrt{1}+(1)^{2}\right ]$

$=a\left [ \sqrt{2}+\log (1+\sqrt{2} )\right ]$

Q2. Find the distance travelled between

$t=0\: and\, t=\frac{\pi }{2}$ by a particle P(x,y) whose position at time t is given by $x=a(\cos t+t\sin t),\: y=a(\sin t-t\cos t).$
Sol.
The position of the particale at time t is given by
$x=a(\cos t+t\sin t),\: y=a(\sin t-t\cos t).$

$\frac{\mathrm{d} x}{\mathrm{d} t}=a\left [ -\sin t +t.\cos t+\sin t.1 \right ]=a\: t\cos t$

$and\frac{\mathrm{d} y}{\mathrm{d} t}=a\left [ \cos t -t(-\sin t)-\cos t.1 \right ]=a\: t\sin t$

$\therefore \: \: required\: \: distance= \int_{0}^{\frac{\pi }{2}}\sqrt{ \left ( \frac{\mathrm{d} x}{\mathrm{d} t} \right )^{2}+\left ( \frac{\mathrm{d} y}{\mathrm{d} t} \right )^{2}}\, \: dt$

$=\int_{0}^{\frac{\pi }{2}}\sqrt{a^{2}\: t^{2}\: \cos ^{2}t+a^{2}\, t^{2}\: \sin ^{2}t }\: \: dt$

$=a\int_{0}^{\frac{\pi }{2}}t\sqrt{\cos ^{2}t+\sin ^{2}t}\: \: dt$

$=a\int_{0}^{\frac{\pi }{2} }t\: dt=a\left [ \frac{t^{2}}{2} \right ]_{0}^{\frac{\pi }{2}} =\frac{a}{2}\left [ \left ( \frac{\pi }{2} \right )^{2}-(0)^{2} \right ] =\frac{a\pi ^{2}}{8}$

Q3. Find the length of the spiral $r=a\: e^{\Theta \cot \alpha }$ between the points at which the radii vector are $r_{1}\: and\: r_{2}.$
Sol.
The equation of curve is $r=a\: e^{\Theta \cot \alpha }$

$\frac{\mathrm{d} r}{\mathrm{d} \Theta }= a\: e^{\Theta \cot \alpha }.\cot \alpha$

$r\frac{\mathrm{d} \Theta }{\mathrm{d} r}=r\frac{1}{\frac{dr}{d\Theta }} =a\: e^{\Theta \cot \alpha }\frac{1}{ a\: e^{\Theta \cot \alpha} \cot \alpha }=\tan \alpha$

$\therefore \: \: length of arc = L=\int_{r_{1}}^{r_{2} }\sqrt{1+r^{2}\left ( \frac{\mathrm{d} \Theta }{\mathrm{d} r } \right )^{2}}\, \: dr =\int_{r_{1}}^{r_{2}}\sqrt{1+\tan ^{2}\alpha }\, \: dr$

$=\int_{r_{1}}^{r_{2}}\sec \alpha .dr=\sec \alpha \left [ r \right ]_{r_{1}}^{r_{2}}=(r_{2}-r_{1})\sec \alpha$ .

Friday, 22 March 2019