Asymptotes ~ Easy to understand maths

A straight line L is called an asymptotes of an infinite branches of a curve if the perpendicular distance of a point P on that branch from the straight line L tend to zero as P moves to infinity along the branch. An asymptote of a curve is a line to which the curve converge. In other words, the curve and its asymptotes get infinity close but they never meet. They are use in graphing rational equation.

In most cases, the asymptotes of a curve can be found by taking the limit of a value where the function is not defined. Typical examples would be and or the point where the denominator of a rational function equals zero. Asymptotes are broadly classified into three categories
1. Horizontal asymptote
2. Vertical asymptote
3. Oblique asymptote

1. Horizontal asymptote

Horizontal asymptote is a line which is parallel to x-axis. When x goes to infinity then curve approaches some constant value.

2. Vertical asymptote

Vertical asymptote is a line which is parallel to y-axis. When x goes to infinity then curve approaches some constant value.

3. Oblique asymptote

An asymptote, which is neither parallel to x-axis nor y-axis is called an oblique asymptote. When x goes to infinity then curve goes toward a line y=mx+c.

☆Rule to find asymptotes parallel to x-axis

Equate to zero the real linear factor in the coefficient of higher power of x in the equation of the given curve.
It should be noted properly that if coefficient of higher power of x in the equation of the given curve is a constant or has no real linear factor, then the curve has no asymptote parallel to x-axis.

☆Rule to find asymptotes parallel to y-axis

Equate to zero the real linear factor in the coefficient of higher power of y in the equation of the given curve.
It should be noted properly that if coefficient of higher power of y in the equation of the given curve is a constant or has no real linear factor, then the curve has no asymptote parallel to y-axis.

Example

Q1. Find the vertical and horizontal asymptotes of the curve $3xy+5x-4y-3=0$
Sol.
The equation of the given curve is $3xy+5x-4y-3=0$ (1)
The coefficient of highest power of x in (1) is $3y+5$

$3y+5=0$ is the only asymptote parallel to x-axis
Horizontal asymptote of given curve is

$3y+5=0$

The coefficient of highest power of y in (1) is

$3x-4$

$3x-4=0$ is the only asymptote parallel to y-axis
Vertical asymptote of the given curve is $3x-4=0$ .

Oblique asymptotes

Rule to find oblique asymptotes

(1). Find $\lim_{x\rightarrow \infty }\frac{y}{x}$ is the equation of the curve and denote it by m.

(2). Find $\lim_{x\rightarrow \infty } \left ( y-mx \right )$ in the equation of the curve and denote it by c.

Then $y=mx +c$ is an asymptote of the curve $f\left ( x,y \right )=0$ .

Example

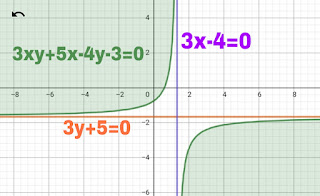
Q2. Find the asymptotes of the curve $y=\frac{x^{2}+2x-1}{x}$ .
Sol.
Here equation of the curve is $y=\frac{x^{2}+2x-1}{x}$
Or $xy=x^{2}+2x-1$
Or $x^{2}-xy+2x-1=0$
The coefficient of highest power of x is 1, which is constant.
Given curve has no asymptote parallel to x-axis

The coefficient of highest power of y is -x
The asymptote of given curve parallel to y-axis is -x=0 or x=0
Let us now find the oblique asymptote $y=mx +c$ .
To determine m and c :
$m =\lim_{x\rightarrow \infty }\frac{y}{x}=\lim_{x\rightarrow \infty }\frac{x^{2}+2x-1}{x}=\lim_{x\rightarrow \infty }\left ( 1+\frac{2}{x} -\frac{1}{x^{2}}\right )=1$
$c=\lim_{x\rightarrow \infty }\left ( y-mx \right )=\lim_{x\rightarrow \infty }\left ( \frac{x^{2}+2x-1}{x}-1.x \right )$
$=\lim_{x\rightarrow \infty }\frac{x^{2}+2x-1-x^{2}}{x}=\lim_{x\rightarrow \infty }\frac{2x-1}{x}$
$=\lim_{x\rightarrow \infty }\left ( 2-\frac{1}{x} \right )=2-0=2$
Therefore oblique asymptote is given by

$y=x+2$
Hence the given curve has two asymptotes given by $x=0$ and $y=x+2$ .

☆Rule to find the asymptotes of a rational algebraic curve :

Step1. Find   $\phi _{n}\left ( m \right ),\phi _{n-1}\left ( m \right )$ by putting x=1 and y=m in the nth degree terms and in the (n-1)th degree respectively of the given curve $f\left ( x,y \right )=0$ .

Step2. Find all real roots of   $\phi _{n}\left ( m \right )=0$ .

Step3. If m₁ is non-repeated root of   $\phi _{n}\left ( m \right )=0$ , then the corresponding to the value of c is given by $c\, \phi _{n}'\left ( m \right )+\phi _{n-1}\left ( m \right )=0$ , provided   $\phi _{n}'\left ( m_{1} \right )\neq 0$
If   $\phi _{n}'\left ( m_{1} \right )\neq 0$ , then there is no asymptote to the curve corresponding to the value m₁ of m.

Step4. If m₁ is a repeated root occurring twice, then corresponding values of c are given by

$\frac{c^{2}}{2!}\: \phi ''_{n}\left ( m \right )+c\: \phi '_{n-1}\left ( m \right )+\phi _{n-2}\left ( m \right )=0$ provided

$\phi ''_{n}\left ( m _{1}\right )\neq 0.$
In this case there are two parallel asymptotes to the curve.
Similarly we can proceed when m₁ is repeated three or more times.

Example

Q3. Find the asymptotes of the curve

$x^{3}+2x^{2}y-xy^{2}-2y^{3}+xy-y^{2}-1=0$ .
Sol.
The equation of given curve is $x^{3}+2x^{2}y-xy^{2}-2y^{3}+xy-y^{2}-1=0$ (1)
The coefficient of highest power of x in (1) is 1, which is constant.
There is no asymptotes parallel to x-axis
The coefficient of highest power of y in (1) is -2, which is constant
There is no asymptotes parallel to y-axis

For oblique asymptotes

[Putting x=1 and y=m in degree 3 term]
$\phi _{3}\left ( m \right )=1+2m-m^{2}-2m^{3}$
$\phi _{2}\left ( m \right )=m-m^{2}$
$\phi _{1}\left ( m \right )=0$
$\phi _{0}\left ( m \right )=-1$
Now $\phi _{3}\left ( m \right )=0$

$\therefore \: \: \, \: 1+2m-m^{2}-2m^{3}=0$
$\Rightarrow 1\left ( 1+2m \right )-m^{2}\left ( 1+2m \right )=0$
$\Rightarrow \left ( 1-m^{2} \right )\left ( 1+2m \right )=0$
$\Rightarrow \left ( 1-m \right )\left ( 1+m \right )\left ( 1+2m \right )=0$
$\therefore\, \, \, m=1,-1,-\frac{1}{2}$
$\phi' _{3}\left ( m \right )=2-2m-6m^{2}$
When m=1, $c=-\frac{\phi _{2}\left ( m \right )}{\phi' _{3}\left ( m \right )}=\frac{\phi _{2}\left ( 1 \right )}{\phi '_{3}\left ( 1 \right )}=-\frac{1-1}{2-2-6}=0$
Corresponding asymptotes is y=x, or x-y=0

When m=-1,

$c=-\frac{\phi _{2}\left ( m \right )}{\phi' _{3}\left ( m \right )}=\frac{\phi _{2}\left ( -1 \right )}{\phi '_{3}\left ( -1 \right )}=-\frac{-1-1}{2+2-6}=\frac{-2}{-2}=-1$
Corresponding asymptotes is y=-1x-1 i.e., x+y+1=0

When $m=-\frac{1}{2},$

$c=-\frac{\phi _{2}\left ( m \right )}{\phi' _{3}\left ( m \right )}=\frac{\phi _{2}\left ( -\frac{1}{2} \right )}{\phi '_{3}\left ( -\frac{1}{2} \right )}=-\frac{-\frac{1}{2}-\frac{1}{4}}{2+1-\frac{3}{2}}=\frac{\frac{3}{4}}{\frac{3}{2}}=\frac{1}{2}$
Corresponding asymptotes is $y=-\frac{1}{2}x+\frac{1}{2}\: \, \: i.e,\: \, x+2y=1$

Hence asymptotes of the given curve are

$x-y=0,\: \: x+y+1=0,\, \: x+2y=1$

Thursday, 7 March 2019

Asymptotes

1. Horizontal asymptote

2. Vertical asymptote

3. Oblique asymptote

☆Rule to find asymptotes parallel to x-axis

☆Rule to find asymptotes parallel to y-axis

Example

Oblique asymptotes

Rule to find oblique asymptotes

Example

☆Rule to find the asymptotes of a rational algebraic curve :

Example

0 comments:

Post a Comment

Popular Posts

Categories

About Me

Contact Us

Blog Archive

Search This Blog

Labels

Recent Post

Pages

Popular Posts