A curve's Inflection point is the point at which the curve's concavity changes. A point that separates the convex part of the curve from part of the curve is called a point of inflexion.
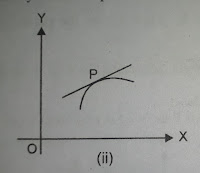
Consider the curve y=f(x) in [ a,b ]. Let it be continuous and possessing tangent at every point in ( a,b ).Draw a tangent at any point P ( c,f(c) ) on the curve. Let us assume that this tangent is not parallel to Y-axis so that f'(c) is some finite number.
Point Of Inflection
The portion of the curve on the two side of P lies on different side of the tangent at P i.e, the curve crosses the tangent at P. In this case we say that P is a point of inflection on the curve.
So, at a point of inflection the curve change from concave upward so convex downward or vice-versa.
So at a point of inflexion f''(x)=0.
☆Working Method Of Find The Point Of inflection
(1). Evaluate(2). Find the value of x which satisfy
Such values x=a,b,c,....(say) are the possible point of inflection.
(3). x=0 will be point of inflection
If (1). Either
or(2).
Note1.
Note2. If at a point, x=c,
Note3. If at a point, x=c,
Example
Q1. Find the point of inflection on the graphs of the functionSol.
Now
x=0 is not a point of inflection.